Ein drittes, sehr kreatives, Lehrszenario zur Nutzung von Smartphones und Tablets im Unterricht, haben sich weitere Studierende der Lehrveranstaltung »Multimediale Lernumgebungen« ausgedacht. Den klassischen Versuch, die Federkonstante zu bestimmen haben sie so abgewandelt, dass ein an der Feder auf und ab schwingendes Mikrofon die Signale eines darunter liegenden Sinuston-Generators aufnimmt. Zur Analyse der Periodendauer einer Schwingung wird die durch die Schwingung verursachte Veränderung der Lautstärke des Signals nutzbar gemacht. Zum Einsatz kommen hier die Apps Signalscope als Tongenerator und die App iAnalyzer zur Auswertung der akustischen Daten. Alle verwendeten Apps wurden auf der Learners´ Garden Plattform beschrieben und verlinkt. Dieses Szenario ist Teil einer Reihe von Lehrszenarien zu denen auch die Szenarien zur Fallbeschleunigung gehören: „Atwood´sche Fallmaschine“ , „Der schiefe Wurf“.
|
|
|
|
Schwingende Feder
Die Untersuchung der Eigenschaften einer schwingenden Feder hat viele Aspekte. Hier geht es darum festzustellen, welcher Zusammenhang besteht, zwischen der Periodendauer, mit der die Feder schwingt und der Masse, die an ihr hängt. Zur Messung der Periodendauer soll ein mitschwingendes Mikrofon einen konstanten Sinuston aufzeichnen.
|
|
|
Sinuston generieren
Dazu wird an der Feder, neben der Masse, das Mikrofon befestigt. Hier: das im Kabel des Kopfhörers integrierte Mikrofon eines iPhones. Unter der schwingenden Masse wird ein Aktivlautsprecher positioniert, der einen Sinuston ausstrahlt. Der Sinuston wird durch die App Signalscope an einem iPad erzeugt, das mit dem Aktivlautsprecher verbunden ist.
|
|

|
Signal aufzeichnen
Das Mikrofon ist an ein weiteres iPad angeschlossen, auf dem die App iAnalyzer aktiv ist. Die Feder wird in Schwingung versetzt, das Mikrofon eingeschaltet und das Signal wird einige Sekunden lang aufgezeichnet. Durch scrollen durch den aufgezeichneten Sample per touch, lassen sich millisekundengenau die Peaks des Samples ermitteln und damit die Periodendauer der Schwingung.
|
|

|
Verschiedene Massen
Die Ermittlung der Periodendauer auf diese Art wird für unterschiedliche Massen durchgeführt. Nach auswechseln der anhängenden Masse und Protokollierung der gemessenen Daten wird die nächste Messung mit der jeweils nächsten Masse durchgeführt.
|
|

|
Mögliche Zusammenhänge
Bei Vorliegen aller Daten werden verschiedene mögliche Zusammenhänge zwischen Periodendauer und Masse aus den gemessenen Daten errechnet, z.B:
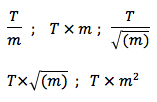
|
|

|
Proportionaler Zusammenhang
Beim Durchrechnen wird irgendwann auffallen, dass der Wert
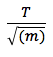
unabhängig vom Gewicht der Masse, konstant bleibt. Dadurch wird ersichtlich, dass bei der Federschwingung das Quadrat der Periodendauer proportional ist zur Masse.
|
|
|
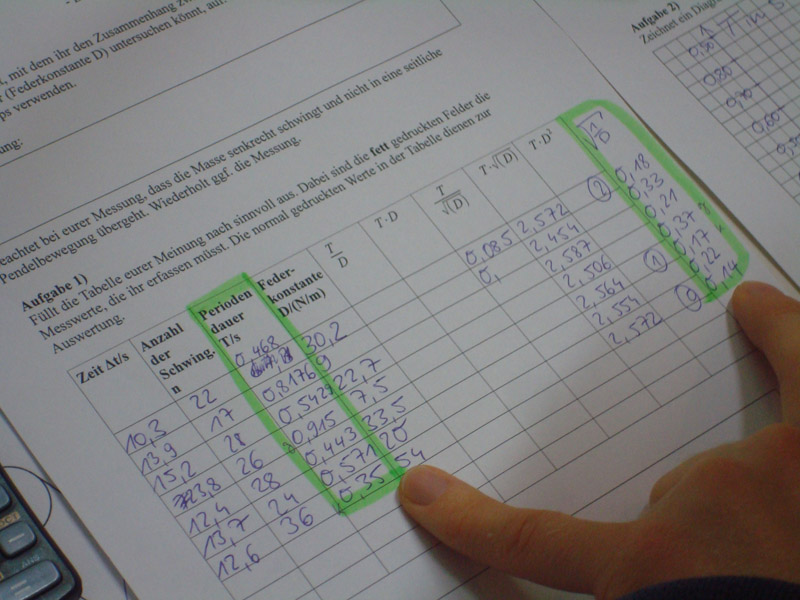
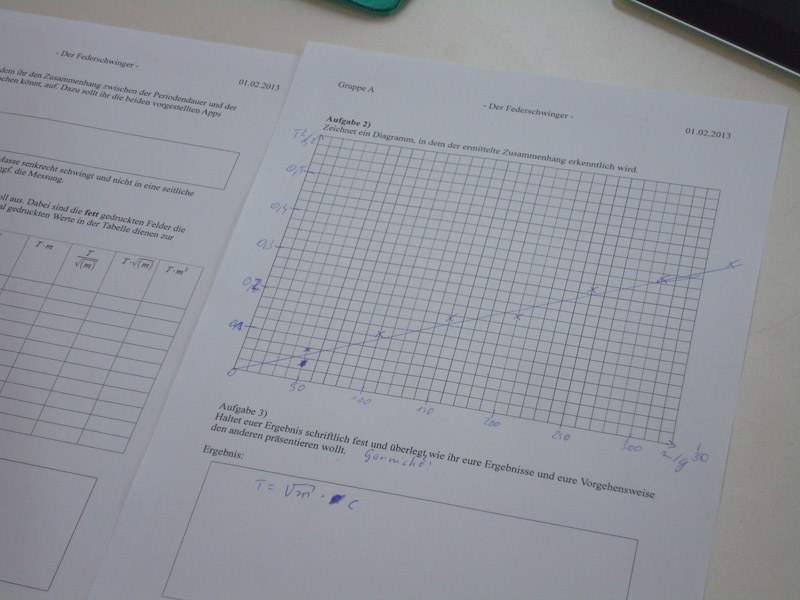
Graph
Diesen Zusammenhang stellen die Schüler anschließend graphisch dar, indem sie das Quadrat der Periodendauer über der Masse in einem Koordinatensystem abtragen und dort die abgeleiteten Werte eintragen. Es ergibt sich eine Gerade, die den proportionalen Zusammenhang auch graphisch anschaulich macht.
|
|
|




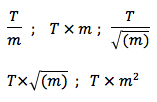




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.